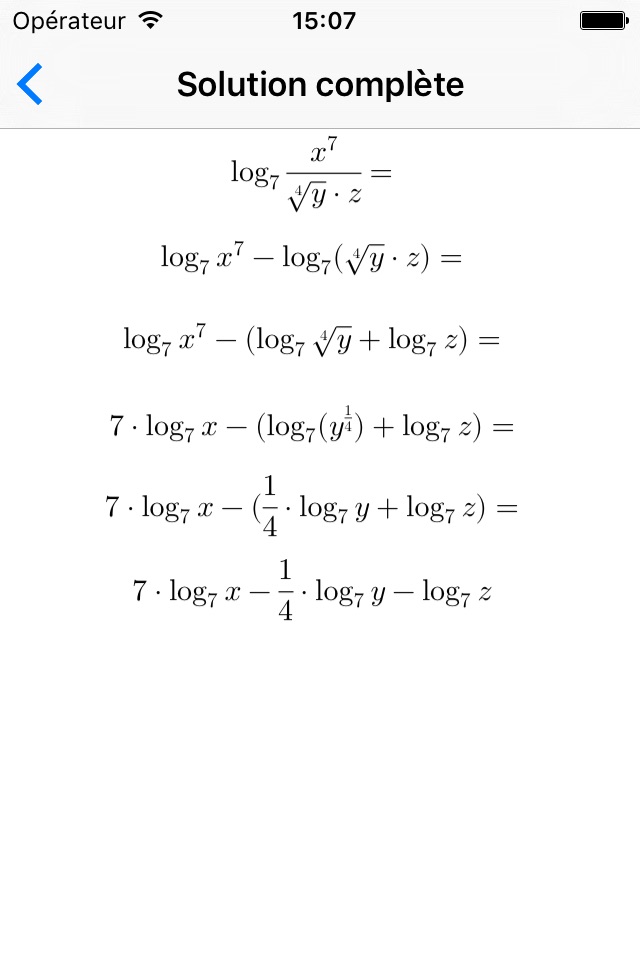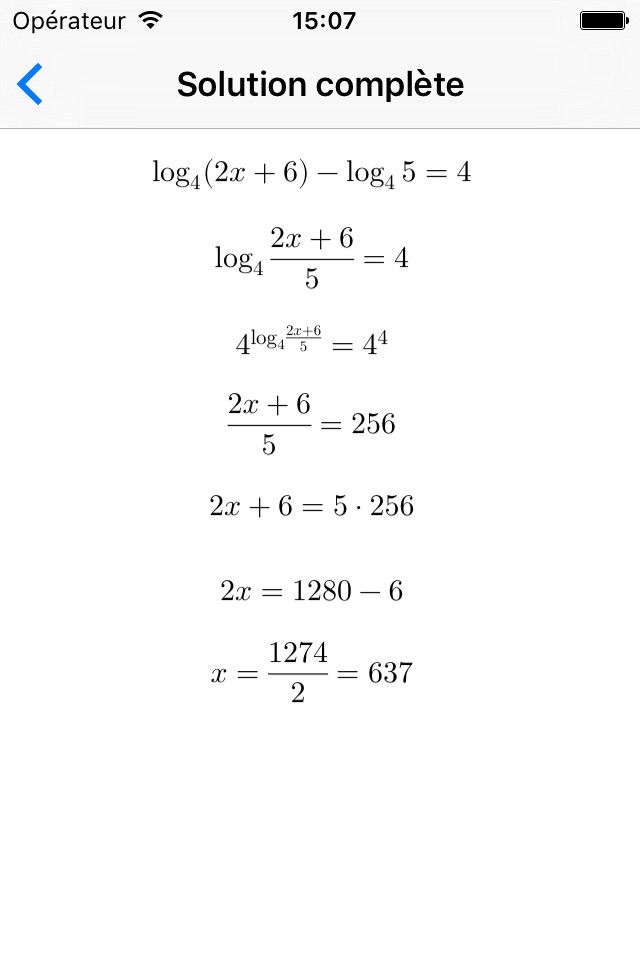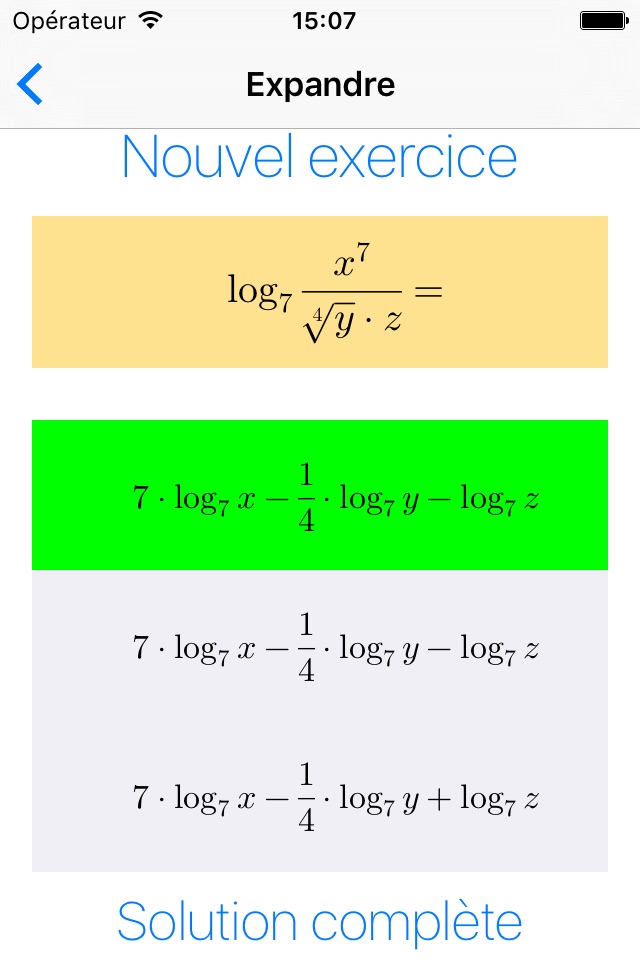
• App per imparare i LOGARITMI.
• La app crea delle equazioni e delle espressioni logaritmiche SEMPRE DIVERSE e MOSTRA LA SOLUZIONE COMPLETA!!!
• Uno strumento ideale per lo studio della matematica nelle scuole medie superiori e nelle scuole tecniche.
• É inoltre possibile esercitare le regole di calcolo per i logaritmi (semplificare ed espandere delle espressioni ). Fondamentali per riuscire a risolvere le equazioni.
• Contiene inoltre una calcolatrice per il calcolo dei logaritmi in qualsiasi base.
• Funziona 100% offline
• Adatta anche per professori che devono creare equazioni logaritmiche come compito per gli studenti.
• 5 livelli sono disponibili:
1) Semplifica (Gratis)
2) Espandi (Gratis)
3) Equazioni - Facile (Gratis)
4) Equazioni - Medio (Acquisto in-app)
5) Equazioni - Difficile (Acquisto in-app)
• Semplifica: applicazione delle regole di calcolo dei logaritmi per compattare le espressioni
p.es. log(5)+log(4)-log(2)=log(5*4/2)=log(10)
• Espandi: lopposto di semplifica, p.es. log(x*y/(2z))=log(x*y)-log(2z)=log(x)+log(y)-[log(2)+log(z)]=log(x)+log(y)-log(2)-log(z)
• Equazioni - Facile: qui vengono presentate delle equazioni che richiedono semplicemente lapplicazione della definizione di logaritmo e lapplicazione delle regole di calcolo, sono risolvibili in pochi passaggi e rappresentano unottimo punto di partenza per le equazioni più
difficili.
• Equazioni - Medio: in questo livello vengono presentate delle equazioni che richiedono un numero più elevato di passaggi per essere risolte. Padroneggiando questo livello é possibile ottenere dei risultati medio/buoni ad un esame.
• Equazioni - Difficile: questo é un livello dove vengono presentate equazioni logaritmiche che conducono ad equazioni quadratiche mediante un sostituzione di variabile, il numero di passaggi necessario per risolverle aumenta ancora rispetto al livello medio. Vengono inoltre presentate delle equazioni con logaritmi in basi diverse e equazioni che richiedono unottima conoscenza del tema. Padroneggiando questo livello un ottimo risultato allesame é altamente probabile :-)